Schedule Generation via Graph Traversal

Introduction

At Tabernacle Baptist Church in Raleigh, NC, where I’m an active member, I’m in charge of scheduling people to stand at the entryway and ensure visitors are welcomed and directed to where they need to go. When I first took on this responsibility I thought it would be trivial since I only needed to schedule one person a week and do my best to not schedule the same person two weeks in a row. Easy…right?

As you might have guessed nothing is that simple. If those had been the only constraints I likely wouldn’t be writing this post. As I started building schedules I quickly realized that people have lives (and other commitments to the church) that would make this less trivial than I initially thought. There may be scheduling conflicts with other teams, people may be out of town for multiple weeks at a time, or there may be schedules from other teams that don’t necessarily conflict with our own but put unnecessary burden on members when they’re added to our schedule. In addition, I’m not the only one building schedules nor is this something I have to do only once. If I automate it, it can be shared with others to ease their burden and the schedules they build could even be fed back into the system so schedules from other teams won’t conflict.

So, let’s dive in and look at the steps I took to build an automated scheduling solution as well as the hurdles I encountered. The intent behind this post is to walk you through the steps of understanding a problem and thinking through how to solve it algorithmically. As such I include only relevant code snippets in each section.

Constraints

Before we look at the process of building an algorithm let’s understand our constraints in this problem. To build a “fair” schedule we will need to adhere to the following:

1. Members will not be scheduled on their “blackout” dates - dates on which they will not be available.
2. Members will not be scheduled in a way that will conflict with other schedules to which they’re assigned.
3. Member assignments will be evenly distributed across a schedule. Assigning a member to a slot becomes more acceptable the further out that slot is from their last assignment.

We’ll need to make sure our algorithm accounts for these simultaneously.

First Attempt

I’ll admit my first attempt at a solution was a bit naive. This was primarily due to time constraints which required me to build some schedules immediately. It was sufficient for the time but, as I would later discover, it would not scale well.

I decided to go with a queue-based approach. The basic algorithm works like this:

1. Iterate over the list of days.
2. For each day, enumerate the list of members checking if each one can be scheduled on the given day.
3. Schedule the first available member and move them to the back of the queue.
4. Loop

# Days populated elsewhere
days = [...]
# Member queue populated elsewhere
queue = [m1, m2, m3]
# Blank schedule
schedule = []

# Iterate over the list of days
for day in days:
    can_schedule = False
    member = None

    # Enumerate the queue checking who can be scheduled
    for idx, tmp_member in enumerate(queue):
        if day in tmp_member["blackouts"]:
            continue
        can_schedule = True
        queue.pop(idx)
        member = tmp_member
        break

    # If no one can be scheduled raise an error
    if not can_schedule:
        raise RuntimeError(f"Failed to schedule anyone for {day}")
    
    # Update the schedule
    schedule.append({"date": day.strftime("%m/%d/%y"), "member": member["name"]})

    # Readd the member to the back of the queue
    queue.append(member)

return schedule

This works well and fairly quickly but has some issues that may not be obvious at first glance. There are some things I’m not showing you for the sake of brevity, such as how the member list is populated. That may seem insignificant but it matters very much. Consider the effect our constraints have on the resulting schedule with regard to the order in which we enumerate our member list. We may end up with an “unfair” schedule due to an assignment we made early on that excluded the member from being scheduled again. That sounds a bit confusing so let’s look at an example.

Assume we have three members [m1, m2, m3] and three days [d1, d2, d3] to schedule. Assuming no one has any blackouts or conflicts then any permutation of members to days is valid. However, what if m2 and m3 have a blackout on d2? The resulting schedule would be {d1: m1, d2: m1, d3: m2}! Not only would m1 be scheduled two times in a row but m3 wouldn’t be scheduled at all, breaking two of our constraints. To put it another way, we can’t always start with m1 to build our schedules. To solve this issue we can run the algorithm over all permutations of the list.

Addressing All Permutations

Since it matters which member we start with does it also matter which member is in the second, third, and fourth indexes of the list? As it turns out, yes. Each day we schedule is just a subset of the whole problem. This means we must build a schedule for every permutation of the members queue. We can do this easily in Python with the permutations function from itertools.

from itertools import permutations

members_lists = list(permutations(["m1", "m2", "m3"]))
for ml in members_lists:
    build_schedule(ml)

## Output
# ('m1', 'm2', 'm3')
# ('m1', 'm3', 'm2')
# ('m2', 'm1', 'm3')
# ('m2', 'm3', 'm1')
# ('m3', 'm1', 'm2')
# ('m3', 'm2', 'm1')

Now we can build all possible schedules and pass them to other functions to determine which are the most “fair”. However, while this solves one problem it introduces another with regard to scalability.

Scalability Issues

Now that we’re building schedules based on all permutations the system has a lot more work to do. The number of schedules that will be built is m! where m is the number of members. This isn’t much of an issue until we get to about 9 or 10 members (depending on how many days we need to schedule). 10! is 3,628,800. That’s a lot of schedules to churn through and even a beefy system won’t complete it in a reasonable time. Here is the output of the time command when this code is run with 9 members:

15.10s user 0.34s system 99% cpu 15.456 total

15 seconds is practically an eternity in computing. When running the same code with 10 members the execution never even completes! At this point we’ve added a basic sense of fairness to the code but it has introduced a hard limit on our inputs. We need to come up with a better algorithm to speed up the process and allow it to scale.

Iterate

In computational complexity theory there is a concept known as reduction in which we can convert a problem with high computational complexity into a well-known problem with low computational complexity. This also works if you have a problem you don’t know how to solve but can figure out a way to frame it as one for which you already have a solution.

Given all of our constraints and the difficulty of building m! schedules, what if we just reduced this to a graph traversal problem? Then we could represent all possible schedules in the graph and just follow the path from root to goal for the most efficient (or “fair”) path. By reducing the problem to a graph we also get some other benefits such as the ability to memoize solved structures and prune inefficient paths.

Let’s take a look at our earlier example with three members and three days. Here is a graph that represents all possible permutations given a single member to start as our root node. If we wanted to cover all possible schedules we would need to build m graphs starting with each member in the list.

graph TD;
    root-->d2-m1;
    root-->d2-m2;
    root-->d2-m3;
    d2-m1-->d3-m1;
    d2-m1-->d3-m2;
    d2-m1-->d3-m3;
    d2-m2-->d3'-m1;
    d2-m2-->d3'-m2;
    d2-m2-->d3'-m3;
    d2-m3-->d3"-m1;
    d2-m3-->d3"-m2;
    d2-m3-->d3"-m3;

Searching the graph with our eyes we can see there are exactly two paths we would consider to be “fair” for any given root node. e.g. if root is m1 then the fairest paths are [root] -> [d2-m2] -> [d3'-m3] and [root] -> [d2-m3] -> [d3"-m2]. But there are nine possible solutions which means there are seven we shouldn’t waste our time processing if we can help it.

Talking about wasted time, the search space is growing rapidly. In fact, you may have noticed there are more than m! solutions when you combine this graph with the others we would need to build for each of our members to start in the root node. The total number of nodes across all graphs which we would potentially visit is represented by the equation below where d is the depth minus 1 (or number of days zero-indexed) and m is the number of members.

\[\LARGE m*\sum_{x=0}^{d}m^x\]

If we were to run the algorithm across the entire graph we’ll find it actually performs worse than our queue-based approach. Fortunately, there are some things we can do to limit the search space which we’ll talk about in Traversing the Graph. Before we can do that we first have to build the graph.

Building the Graph

If we’re not careful, building our graph could take so long that we’ll terminate our program before it even begins searching. If we build it node-by-node without optimizations we’ll run into the same scalability issues we had with the queue-based approach. To avoid these problems we’re going to use memoization to prevent rebuilding sub-trees that have already been built. The graph below shows how memoization can help us:

graph TD;
    root-->d2-m1;
    root-->d2-m2;
    root-->d2-m3;
    d2-m1-->d3-m1;
    d2-m1-->d3-m2;
    d2-m1-->d3-m3;
    d2-m2-->d3-m1;
    d2-m2-->d3-m2;
    d2-m2-->d3-m3;
    d2-m3-->d3-m1;
    d2-m3-->d3-m2;
    d2-m3-->d3-m3;

Notice that we have all the same paths as the previous graph but fewer nodes. As we add more members and days to the input this approach will keep the work required to build the graph to a minimum. See the code below (specifically lines 7-8 and 40) for a recursive function that builds this graph. Don’t worry about the custom classes used here; an Entry is just a node in the graph and a Person represents a member.

def populate_graph_r(
    people: list, person: Person, days: list, day: datetime, ref_time: dict
) -> Entry:
    day_pos = days.index(day)

    # Lookup in cache
    if (day, person) in memoize_cache:
        return memoize_cache[(day, person)]
    
    # If the person cannot be scheduled on the current day
    # there is no need to build the tree further
    if not person.can_schedule(day, ref_time):
        return None
    
    # Create a new Entry (node) and add the
    # person to it.
    entry = Entry(day)
    entry.person = person
    entry.depth = day_pos + 1

    # Check if we are on the last day in the list
    if day_pos + 1 < len(days):
        # For each person, recurse to the next day
        for _p in people:
            # Recurse and continue building the graph
            next_entry = populate_graph_r(people, _p, days, days[day_pos + 1], ref_time)

            # If the child node could not be established
            # then skip it. Otherwise, append it to the
            # current node's list of children.
            if next_entry:
                entry.next.append(next_entry)
    else:
        # Mark this entry as a leaf node meaning there
        # are no children nodes beneath it
        entry.leaf = True

    # Memoize the entry so it can be
    # referenced later
    memoize_cache[(day, person)] = entry

    return entry

Our memoize_cache is a simple dict that we use to store the entry for a day (depth) and person (member). Notice at line 7 how we first perform a lookup to see if a node has already been computed and, if found, is returned before doing any real work. Assume this node is d3-m2 from our graph above. Where previously we would have built it 3 times we now have built it only once and simply pointed to it the other two times. Also, remember our equation above that states we build m number of graphs? To offset this we maintain our cache across graph builds since the subtrees will be the same. This is a significant optimization with regard to speed and storage.

Calculating “Fairness”

We need a way to express fairness so our traversal algorithm can make decisions that are in agreement with our list of constraints. One way this can be done is by associating a cost with each node. This cost will get passed down to each child node so that at any point in the graph we can know how expensive it is to travel there. So let’s define this cost.

• The base cost to travel to a node is 1 in addition to the cost of its parent. i.e. the cost of a node is its total cost from root.
• The cost should be adjusted proportionally to the frequency with which the member has been scheduled thus far. We’ll call this visibility and associate a higher cost with high visibility and lower cost with low visibility.
• The max value for cost will be pinned to m (the number of members).

We might be tempted to store this cost with each node when we build the graph to make traversal easier. However, this will break our memoization optimization as we need different cost values based on which path has led us to a node. Instead, we’ll build an overlay graph as we traverse the original. This overlay will consist of traversal nodes (or tNode) that track visibility of all members as well as the node’s cost. At each depth, the visibility will be updated by the following function:

def update_visibility(ref: dict, entry: str) -> None:
    """
    Sets the visibility to the max for
    the provided entry and decrements
    all others by one
    """
    for key in ref:
        ref[key] = ref[key] - 1 if ref[key] > 0 else 0
    ref[entry] = configs["NUM_MEMBERS"]

When we visit a node we set its cost to the maximum and decrement all others by 1. This way if the node comes up again in our search path before all other members have been scheduled, it will be picked last among its peers. Now that we have a way to determine a “fair” path lets put it to use in the last piece of our puzzle…traversal.

Traversing the Graph

At this point all of the hard work has been done. All that’s left is to hop from node to node traveling down the cheapest path. But how do we know which path will be the cheapest? What if the cheapest path at depth 3 leads to a more expensive path overall by depth 10? Our traversal algorithm will need a heuristic to help guide it to an optimal path. Our heuristic is simple:

\[\large min(childCost + (maxDepth - childDepth), lowestCost)\]

In English, if the least potential cost from the current node to a leaf node is not lower than our current best path then we have no reason to travel down it. This will ensure that our search gets more efficient as it progresses. We’ll also be sure to only identify goal nodes as those that have the lowest cost. If we find a cheaper path to a leaf node we will throw out our previous goal nodes and start fresh.

Putting it all together we get our traverse() function below:

def traverse(entry):
    if not entry:
        return []

    unvisited = [tNode(1, entry, None, {entry.person.name: configs["NUM_MEMBERS"]})]
    goals = []

    while unvisited:
        tnode = unvisited.pop()

        if tnode.node.leaf:
            # If the total cost of the current path is less
            # than the lowest cost so far it becomes our
            # new lowest cost
            if tnode.cost < configs["LOWEST_COST"]:
                configs["LOWEST_COST"] = tnode.cost
                goals = []
            if tnode.cost == configs["LOWEST_COST"]:
                goals.append(tnode)
            # If the lowest cost found so far is equal to the
            # lowest possible cost (number of days) then it's
            # impossible to find a better solution so we break
            # the loop
            if configs["LOWEST_COST"] == configs["NUM_DAYS"]:
                break
        else:
            child_tnodes = []
            for child in tnode.node.next:
                # Build a child tNode
                child_tnode = tNode(0, child, tnode, tnode.visibility.copy())

                # Calculate the cost based on the visibility
                child_cost = child_tnode.visibility.get(child.person.name, 1)
                child_tnode.cost = tnode.cost + child_cost

                # Increase the visibility of the current node
                update_visibility(child_tnode.visibility, child.person.name)

                # Build a heuristic based on the cost from root to this node and
                # how many nodes we have to go until we hit a leaf
                heuristic = child_tnode.cost + (configs["NUM_DAYS"] - child.depth)
                if heuristic < configs["LOWEST_COST"]:
                    child_tnodes.append((child_cost, child_tnode))

            # Push the nodes with the least cost to the heap queue
            if len(child_tnodes) > 0:
                least_cost_child = min(child_tnodes)[0]
                for c in child_tnodes:
                    if c[0] == least_cost_child:
                        unvisited.append(c[1])
    return goals

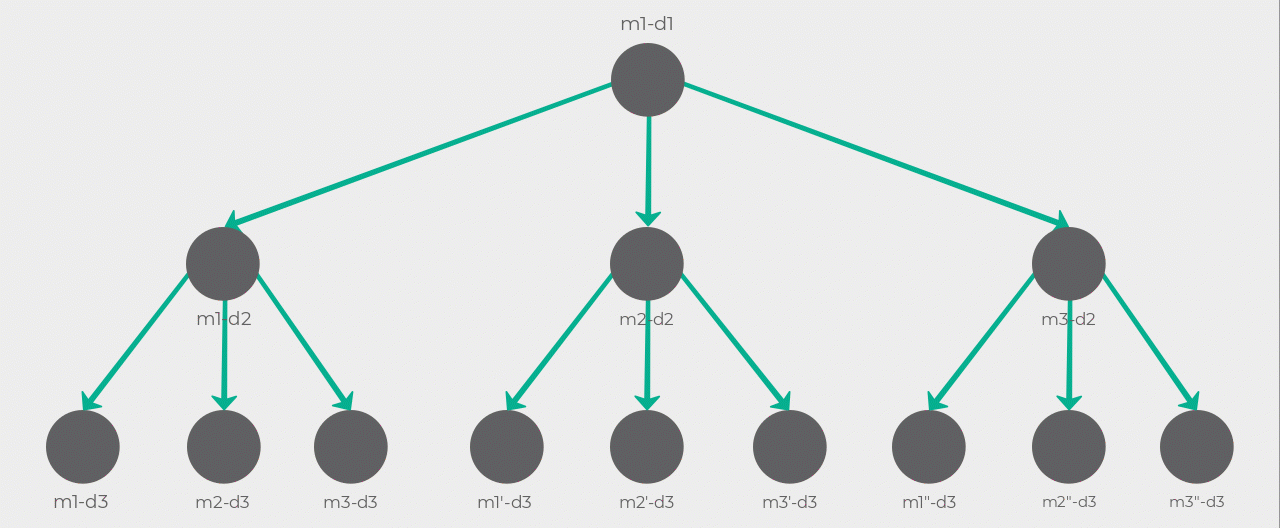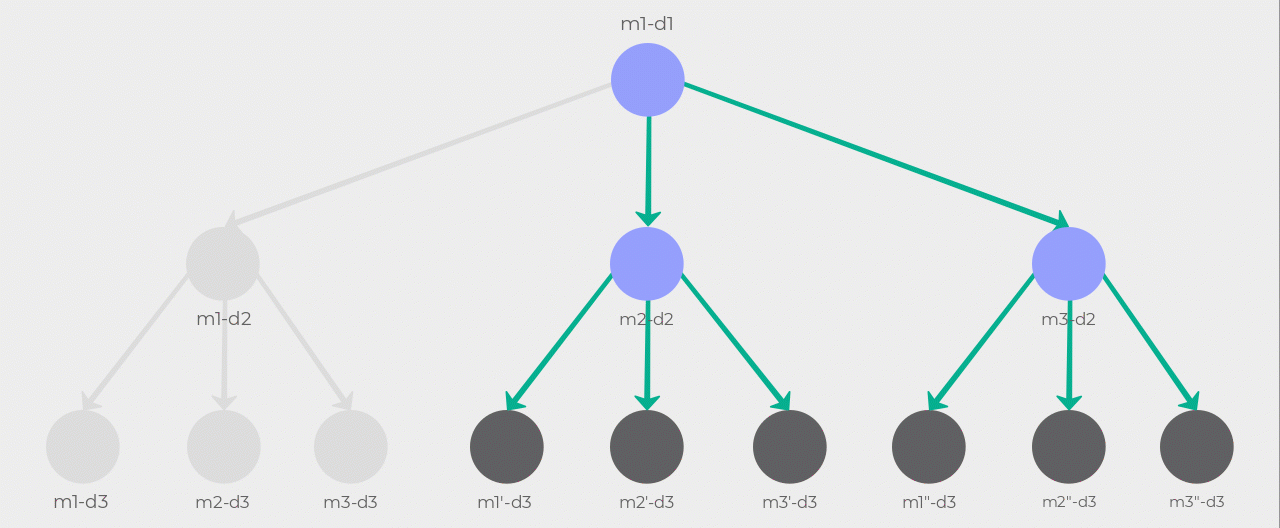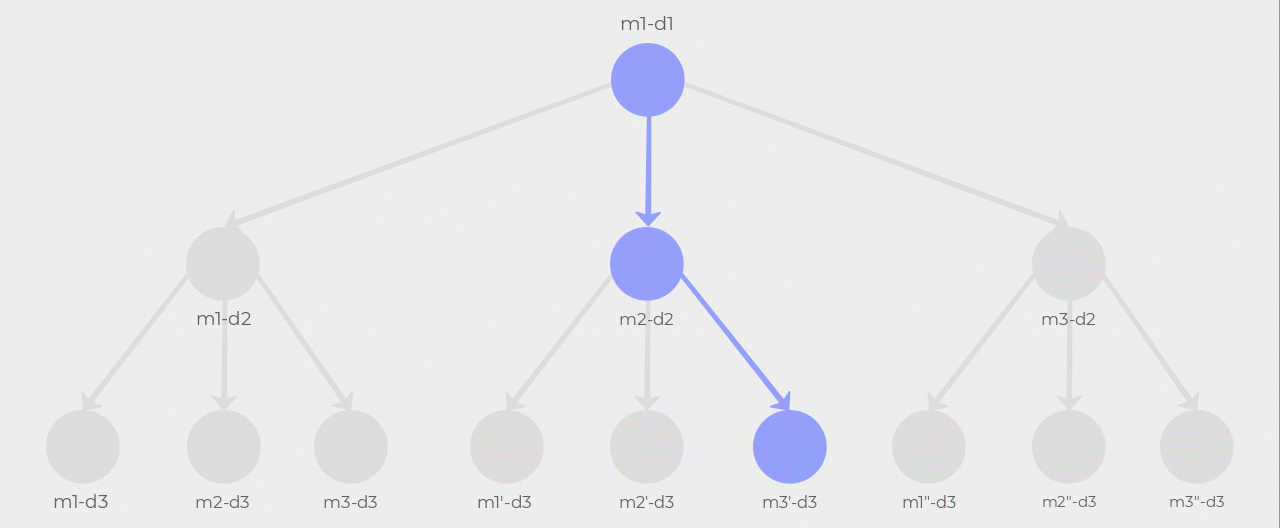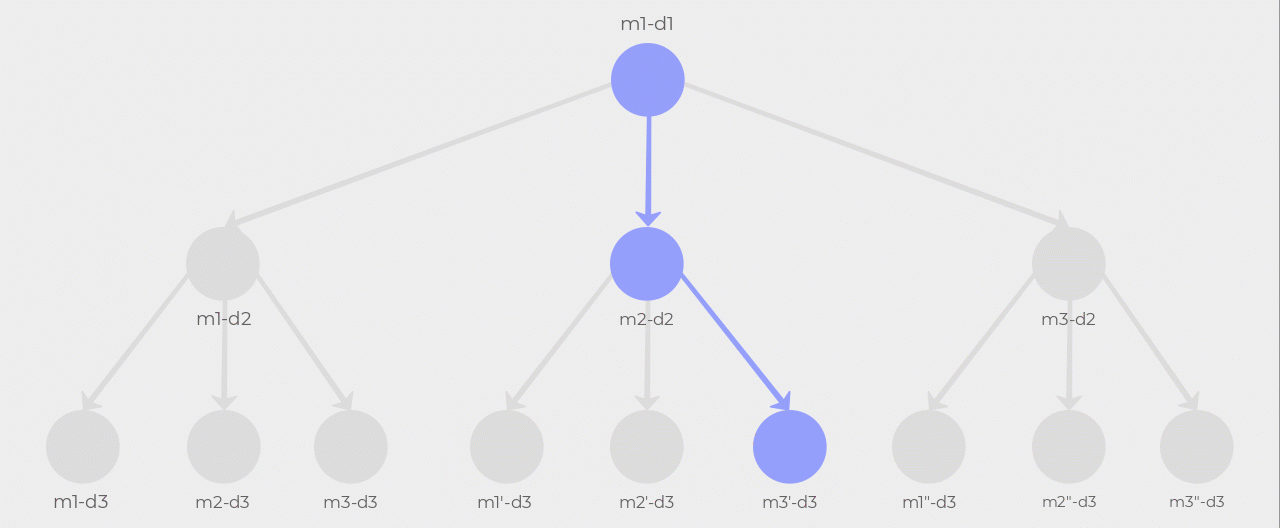
Using our example of three members and three days, the following diagram should help you visualize what’s happening here. Notice how m1-d2 and its children are pruned after m2-d2 and m3-d2 are selected. This is due to the root node being m1 so m1’s visibility is higher than m2 and m3. The algorithm then follows the m2-d2 path and expands its children. Since m1 and m2 have already been selected in the path their visibility is higher than m3 so m3'-d3 gets selected. Now there’s another optimal path from m3-d2 to m2"-d3 but its cost is at best equal to the cost of the path the algorithm just discovered. There is no point in continuing the search so it terminates.

Look at the result of our time function with the same inputs as our earlier example:

0.03s user 0.01s system 93% cpu 0.043 total

Down from 15 seconds to 43 milliseconds is a significant improvement! This was with nine members across four months. Even when scaled up to twenty members across ten years the time to complete barely jumps to just under half a second:

0.41s user 0.02s system 99% cpu 0.431 total

Conclusion

You may have noticed constraint #2 was not covered in this post. This is because we do not need to add any explicit code to ensure there are no schedule conflicts. In fact, that would just overcomplicate the algorithm. Instead, we can use the built-in support for blackout dates to handle this constraint.

This algorithm is part of a larger scheduling application that consists of a web frontend, database, and containerized backend that facilitate the management of teams, members, and schedules. When the backend receives a request to build a new schedule it first pulls all other schedules with overlapping dates and cross-references the assignments with the request’s member list. Everywhere there is a schedule assignment for one of the members, a blackout date is created and added to the request which guarantees no conflicts with the existing schedules.

If you’ve made it all the way to the end, I want to thank you for taking the time to read this post. I hope it has provided some insight into how simply framing a problem in another way can provide significant improvements in its solution. I have many ideas for future posts with regard to cloud architecture, infrastructure as code, container orchestration, and much more that I hope you’ll come back to enjoy.